linear algebra

참고 : 무료 교재 http://www.kms.or.kr/board/list.html?num=6383&start=330&code=absinfo

스칼라 scalar

• 하나의 수치(數値)만으로 완전히 표시되는 양
• 방향의 구별이 없는 물리적 수량
• 질량·에너지·밀도(密度)·전기량(電氣量) 등
• 1, 3.14, -5, 1.2e5

import numpy as np

a = np.array(1)  # 1차원 배열로 벡터를 나타낸다
print(a.ndim, a.shape)

벡터 vector

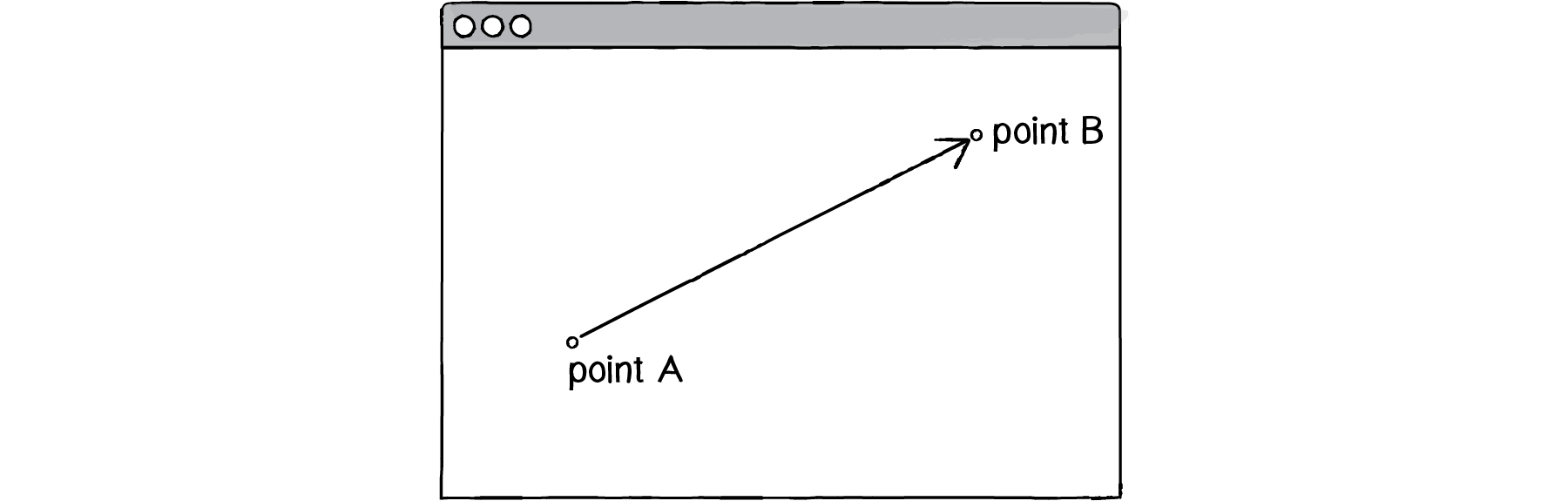
• 벡터는 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성요소
• 물리학에서 말하는 ‘크기와 방향으로 정의되는 값'
• 일반적으로 벡터는 화살표로 표현
• 화살표가 가리키는 쪽은 방향을 나타내며 화살표의 길이는 크기
• 순서를 맞춰 숫자를 나열한 리스트
  • 벡터는 하나의 데이터 포인트라는 관점에서 매우 유용
  • 차원을 무한히 늘릴 수있음
• 수학적으로 가장 의미있는 정의는 벡터란 그저 벡터 공간(vector space)의 원소
• https://angeloyeo.github.io/2020/09/07/basic_vector_operation.html#%EB%B2%A1%ED%84%B0-%EA%B0%84%EC%9D%98-%EC%84%A0%ED%98%95-%EA%B2%B0%ED%95%A9

$$ \vec{q} = (q_1, q_2, ..., q_n) $$

벡터 - numpy 1차원 배열

import numpy as np

a = np.array([1, 2, 3])  # 1차원 배열로 벡터를 나타낸다
print(a.ndim, a.shape)

행렬 matrix

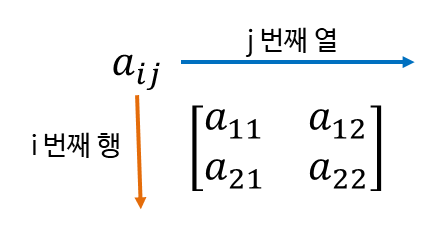
• 수(스칼라) 또는 다항식 등을 직사각형 모양으로 배열한 것
• 수평방향을 행, 수직방향을 열

행렬 - numpy 2차원 배열

import numpy as np

a = np.array([[1, 2, 3],
              [4, 5, 6]])  # 2×3의 행렬
print(a.ndim, a.shape)

텐서 tensor

• Tensor 는 수학과 물리학에서 서로 약간 다른 의미로 사용되는 개념
• 텐서란 매우 수학적인 개념으로 데이터의 배열
• 스칼라를 여러 개의 차원으로 나열한 것

3차원 텐서 - numpy 3차원 배열

import numpy as np

a = np.array([[[0, 1, 2, 3],
                      [2, 3, 4, 5],
                      [4, 5, 6, 7]],

                     [[1, 2, 3, 4],
                      [3, 4, 5, 6],
                      [5, 6, 7, 8]]])  # (2, 3, 4)의 3차원 텐서
print(a.ndim, a.shape)

자연어 처리 예시

# Hi Foo
# Hi Bar
# Hi Baz
hi = np.array([1,0,0,0])
foo = np.array([0,1,0,0])
bar = np.array([0,0,1,0])
baz = np.array([0,0,0,1])

# matrix
hi_foo = np.array([hi,king])
hi_bar = np.array([hi,queen])
hi_baz= np.array([hi,jack])

# 3d-tensor
his = np.array([hi_foo, hi_bar, baz])
his.ndim, his.shape

백터의 내적

• 벡테의 각 요소끼리 곱한 값의 총합
• 두 벡터의 요소 수가 동일 해야함
• numpy의 dot()

  $$ \vec{a} = (a_1,a_2,...,a_n) $$

  $$ \vec{b} = (b_1,b_2,...,b_n) $$

  $$ \vec{a} \cdot \vec{b} = (a_1b_1 + a_2b_2 + ... + a_nb_n) $$

  $$ \vec{a} \cdot \vec{b} = \sum_{k=1}^N a_k b_k $$

import numpy as np

a = np.array([1, 2, 3])
b = np.array([3, 2, 1])
r1 = np.dot(a,b)
r2 = np.sum(a*b)

벡터의 크기 : 놈(노름) norm

• numpy의 linalg.norm() 함수
• L1 놈, L2 놈

L2 놈

• 벡터의 각 요소의 제곱합에 제곱근으로 구함

  $$ \lVert \vec{x} \rVert_2 = \sqrt{x_1^2 + x_2^2 + ... + x_n^2} $$

L1 놈

• 벡터의 각 요소의 절대값의 총합으로 구함

  $$ \lVert \vec{x} \rVert_1 = \left\vert x_1 \right\vert + \left\vert x_2 \right\vert + ... + \left\vert x_n \right\vert $$

import numpy as np

a = np.array([1, 1, -1, -1])

print("--- L2놈 ---")
print(np.linalg.norm(a))  # L2놈(디폴트)
print("--- L1놈 ---")
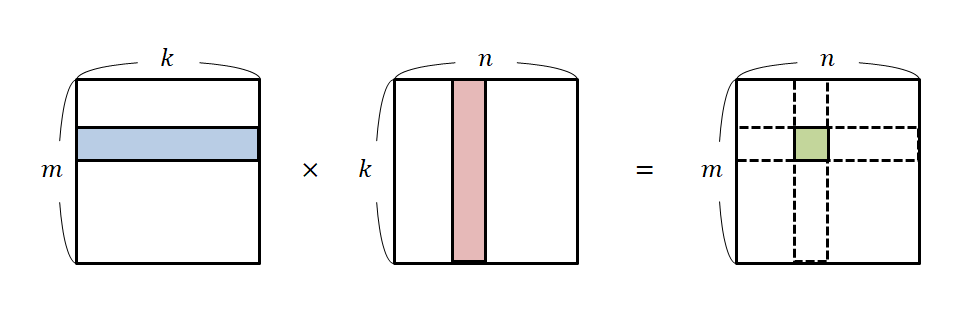
print(np.linalg.norm(a, 1))  # L1놈

행렬의 곱

• 벡터의 내적을 행렬로 확장
• AI에서 많이 사용됨

import numpy as np

a = np.array([[0, 1, 2],
              [1, 2, 3]]) 

b = np.array([[2, 1],
              [2, 1],
              [2, 1]])
r1 = np.dot(a,b)
r2 = np.sum(a*b)

요소별 곱(아다마르 곱)

• 행렬의 각 요소별 곱

import numpy as np

a = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]]) 

b = np.array([[9, 8, 7],
              [6, 5, 4],
              [3, 2, 1]]) 

print(a*b)

행렬 전치

• 행과 열을 바꿈

import numpy as np

a = np.array([[1, 2, 3],
              [4, 5, 6]])  # 행렬

print(a.T)  # 전치

전치와 행렬곱 구현

import numpy as np

a = np.array([[0, 1, 2],
             [1, 2, 3]])  # 2×3의 행렬
b = np.array([[0, 1, 2],
             [1, 2, 3]])  # 2×3의 행렬 이대로는 행렬곱을 할 수 없다

# print(np.dot(a, b))  # 전치하지 않고 행렬곱을 취하면 에러

단위행렬과 역행렬

단위 행렬(항등 행렬)

• 주대각선의 원소가 모두 1이며 나머지 원소는 모두 0인 정사각 행렬
• AE=EA=A, E 대한 항등원
• 행렬곱 결과가 자기 자신

import numpy as np

print(np.eye(2))  # 2×2의 단위 행렬
print()
print(np.eye(3))  # 3×3의 단위 행렬
print()
print(np.eye(4))  # 4×4의 단위 행렬

E = np.eye(2)
A = np.array([[1,2],[3,4]])
A == A.dot(E)

역행렬

• 행렬곱에서 단위행렬이 나오게 하는 행렬
• 역행렬이 존재하지 않는 행렬도 있음
• 역행렬 존재 여부 => numpy linalg.det() 사용
• 역행렬 존재 시 => numpy linalg.inv() 사용

역행렬 존재여부

iimport numpy as np

# 역행렬 존재
a = np.array([[1, 2],
              [3, 4]])
print(a[0,0]*a[1,1] - a[0,1]*a[1,0]) # ad - bc 
print(np.linalg.det(a))  # 행렬식이 0이 되지 않는 경우 

# 역행렬 미존재
b = np.array([[1, 3],
              [1, 3]])
print(b[0,0]*b[1,1] - b[0,1]*b[1,0]) # ad -bc
print(np.linalg.det(b))  # 행렬식이 0이 되는 경우

역행렬 구하기

import numpy as np

# 역행렬 존재
a = np.array([[1, 2],
              [3, 4]])
check = (a[0,0]*a[1,1] - a[0,1]*a[1,0]) # ad - bc 
if check != 0:
    print('a check : ', np.linalg.inv(a))  # 행렬식이 0이 되지 않는 경우 

# 역행렬 미존재
b = np.array([[1, 3],
              [1, 3]])
check = (b[0,0]*b[1,1] - b[0,1]*b[1,0]) # ad -bc
if check != 0:
    print('b check : ', np.linalg.inv(b))  # 행렬식이 0이 되는 경우

선형변환

• 벡터 공간에서 벡터 공간으로 가는 함수로, 그것들 중 벡터 공간의 성질을 보존하는, 즉 선형성을 갖는 함수

quiver() : 벡터 그리기

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline


# 화살표를 그리는 함수
def arrow(start, size, color):
    plt.quiver(start[0], start[1], 
               size[0], size[1], 
               angles="xy", 
               scale_units="xy", 
               scale=1, color=color)

# 화살표의 시작점
s = np.array([0, 0])  # 원점

# 벡터
v = np.array([2, 3])  # 세로 벡터를 나타낸다

arrow(s, v, color="black")

# 그래프 표시
plt.xlim([-3,3])  # x의 표시 범위
plt.ylim([-3,3])  # y의 표시 범위
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.grid()
plt.gca().set_aspect("equal")  # 가로세로비를 같게
plt.show()

선형변환

$$ A = {2 -1 \choose 2 -2} , \hat{a} = {2 \choose 3} $$

$$ \hat{b} = A\hat{a} = A = {2 -1 \choose 2 -2} {2 \choose 3} $$

import numpy as np
import matplotlib.pyplot as plt

a = np.array([2, 3])  # 변환 전의 벡터

A = np.array([[2, -1],
                     [2, -2]])

b = np.dot(A, a)  # 선형변환

print("변환 전의 벡터（a）:", a)
print("변환 후의 벡터（b）:", b)

def arrow(start, size, color):
    plt.quiver(start[0], start[1], size[0], 
               size[1], angles="xy", scale_units="xy", scale=1, color=color)

s = np.array([0, 0])  # 원점

arrow(s, a, color="black")
arrow(s, b, color="blue")

# 그래프 표시
plt.xlim([-3,3])  # x의 표시 범위
plt.ylim([-3,3])  # y의 표시 범위
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.grid()
plt.gca().set_aspect("equal")  # 가로세로비를 같게
plt.show()

표준기저

• 벡터는 표준기저와 상수의 곱의 합으로 표현 가능

  $$ \vec{e}_x = {1 \choose 0}, \vec{e}_y = {0 \choose 1} $$

  $$ \hat{a} = {3 \choose 2} = 2 {1 \choose 0} + 3 {0 \choose 1} = 2\vec{e}_x + 3\vec{e}_y $$

import numpy as np
import matplotlib.pyplot as plt

a = np.array([2, 3])
e_x = np.array([1, 0])  # 표준기저
e_y = np.array([0, 1])  # 표준기저

print("a:", a)
print("e_x:", e_x)
print("e_y:", e_y)

def arrow(start, size, color):
    plt.quiver(start[0], start[1], size[0], 
               size[1], angles="xy", 
               scale_units="xy", scale=1, color=color)

s = np.array([0, 0])  # 원점

arrow(s, a, color="blue")
arrow(s, e_x, color="black")
arrow(s, e_y, color="black")

# 그래프 표시
plt.xlim([-3,3])  # x의 표시 범위
plt.ylim([-3,3])  # y의 표시 범위
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.grid()
plt.gca().set_aspect("equal")  # 가로세로비를 같게
plt.show()

고윳값과 고유벡터

• 머신러닝 주성분 분석 기법에 활용

$$ A\vec{x} = \lambda\vec{x} $$

• 고윳값 스칼라 : $$ \lambda $$
• 고유벡터 : $$ \vec{x} $$
• Numpy의 linalg.eig()함수 사용

import numpy as np

a = np.array([[3, 1],
              [2, 4]])

ev = np.linalg.eig(a)  # 고유값과 고유 벡터를 동시에 구한다

print(ev[0])  # 첫 요소는 고유값 

print()

print(ev[1])  # 다음 요소는 고유 벡터

코사인 유사도

• 코사인 유사도는 두 벡터가 이루는 각도를 통해 유사도를 측정하는 방식
• 코사인의 값은 두개의 벡터 방향이 얼마나 일치하는 지 나타냄

  

  이미지참조: https://goofcode.github.io/similarity-measure

import numpy as np

def cos_sim(vec_1, vec_2):
    return np.dot(vec_1, vec_2) / (np.linalg.norm(vec_1) * np.linalg.norm(vec_2))  

a = np.array([2, 2, 2, 2])
b = np.array([1, 1, 1, 1])  # a와 같은 방향
c = np.array([-1, -1, -1, -1])  # a와 반대 방향

print("--- a와 b의 코사인 유사도 ----")
print(cos_sim(a, b))

print("--- a와 c의 코사인 유사도 ----")
print(cos_sim(a, c))