probability statistics
확률이란
- 모든 경우의 수에 대한 특정 사건이 발생하는 비율
$$ P(A) = {a \over n}$$
- P(A) : 사건 A 가 일어날 확률
- a : 사건 A 가 일어날 경우의 수
- n 모든 경우의 수
동전의 앞(또는 뒤)면이 나오는 확률
- n = 2 {앞면, 뒷면} , a = 1
- P(A) = 1 / 2
주사위의 3이 나올 확률
- n = 6 {1,2,3,4,5,6}, a=1
- P(A) = 1 / 6
주사위 3보다 클 확률
- n = 6 {1,2,3,4,5,6}, a= 3 {4,5,6}
- P(A) = 3 / 6
여사건
- 사건 A에대해 A가 일어나지 않는 사건
$$ P(A) = 1 - P(A) $$
확률로의 수렴
- 많은 시행을 거듭하면 (사건발생수/ 시행수) 가 확률로 수렴
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = []
y = []
total = 0 # 시행 수
num_5 = 0 # 5가 나온 횟수
n = 5000 # 주사위를 던진 횟수
for i in range(n):
if np.random.randint(6)+1 == 5: # 0-5까지의 랜덤인 수에 1을 더해서 1-6으로
num_5 += 1
total += 1
x.append(i)
y.append(num_5/total)
print("확률 = ", 1/6)
plt.plot(x, y)
plt.plot(x, [1/6]*n, linestyle="dashed") # y는 1/6이 n개 들어간 리스트
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.grid()
plt.show()평균값과 기대값
- 평균값과 기대값은 같은 개념
평균값
- 평균은 자료를 요약할 때 사용
- 자료의 중심을 측정
- numpy average()로 계산
$$ \mu = {(x_1 + x_2 + ... + x_n) \over n} $$
$$ \mu = {1 \over n } \sum_{k=1}^N x_k $$
import numpy as np
x = np.array([55, 45, 60, 40]) # 평균을 취하는 데이터
print(np.average(x))기댓값
- 시행에의한 각 값과 그값의 확률의 곱의 총합
$$ E = \sum_{k=1}^N P_kx_k $$
- x 시행 값, P 확률값
제비를 뽑아 80%확률로 100원, 15%확률로 500, 5%의 확률로 1000원 일때의 상금 기댓값
- E = 0.8 100 + 0.15 500 + 0.05 * 1000 = 205
import numpy as np
p = np.array([0.8, 0.15, 0.05]) # 확률
x = np.array([100, 500, 1000]) # 값
print(np.sum(p*x)) # 기대값분산과 표준편차
- 값들이 평균으로 부터 얼마만큼 떨어져 분포하고 있는가를 나타냄
분산
- 분산(variance)은 관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눠서 구한값
- numpy var() 함수 사용
$$ V = {1 \over n } \sum_{k=1}^N (x_k-\mu) $$
import numpy as np
# 분산을 취하는 데이터
x_1 = np.array([55, 45, 60, 40])
x_2 = np.array([51, 49, 52, 48])
# 분산의 계산
print(np.var(x_1))
print(np.var(x_2))표준편차
- 분산의 제곱근
- numpy std() 함수 사용
$$ \sigma = \sqrt{V} $$
import numpy as np
# 표준편차를 취하는 데이터
x_1 = np.array([55, 45, 60, 40])
x_2 = np.array([51, 49, 52, 48])
# 표준편차의 계산
print(np.std(x_1))
print(np.std(x_2))확률변수와 확률분포
결정론적 데이터(deterministic data)
- 생년월일처럼 언제 누가 얻더라도 항상 같은 값이 나오는 데이터
확률적 데이터(random data, probabilistic data, stochastic data)
- 정확히 예측할 수 없는 값
- 여러 조건이나 상황에 따라 데이터값에 영향
- 측정 시에 발생하는 오차등
분포(distribution)
- 확률적 데이터에서 어떠한 값이 자주 나오고 어떠한 값이 드물게 나오는가를 나타내는 정보
- 범주형 데이터의 경우 분포는 카운트 플롯(count plot)으로 시각적으로 표현
- 실수형 데이터의 경우 분포는 히스토그램(histogram)을 사용 시각적으로 표현
기술 통계 descriptive statistics
- 분포를 표현하는 또다른 방법으로 분포의 특징을 나타내는 여러가지 숫자를 계산
- 표본평균, 표본중앙값, 표본최빈값
- 표본분산, 표본표준편차
확률변수
$$ X() = x$$
- 수학적으로 확률공간의 표본을 입력으로 받아서 실수인 숫자로 바꾸어 출력하는 함수
- 출력되는 실수가 데이터의 값
- 확률공간의 표본에는 확률이 할당되어 있음
- 확률변수와 이값의 확률의 대응관계 => 확률분포
- 이산확률변수와 연속확률변수가 있음
이산확률변수
- 확률변수값이 연속적이지 않은 값(정수)
- {남,녀} X(남) = 1, P(남)= 1/2, X(여) = 2, P(여) = 1/2
- 주사위 {1,2,3,4,5,6} X(1) = 1, P(1)= 1/6,..., X(6) = 6, P(6) = 1/6
- 주사위 확률변수와 확률분포 표
| $$ X=x_i $$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$ sum $$ |
|---|---|---|---|---|---|---|---|
| $$ P(X=x_i) $$ | $$ 1\over6 $$ | $$ 1\over6 $$ | $$ 1\over6 $$ | $$ 1\over6 $$ | $$ 1\over6 $$ | $$ 1\over6 $$ | $$1$$ |
이산확률변수
- 연속적이고 무한대의 실수 표본값을 가지는 확률변수
- 모든 표본이 실수인 숫자로 변한다면 모든 사건은 구간사건의 조합으로 표시
정규분포(=가우스 분포)
- 통계학에서 가장 중요한 확률분포
- 모수추정과 가설검정이라는 추리통계를 가능하게 해줌
- 종모양의 정규 곡선, 평균이 중심

- 통계학에서 대표적인 연속 확률분포 => 확률밀도함수(PDF)
- 많은 통계자료들은 정규분포를 따름
- 데이터가 정규분포를 따른다는 가정만으로도 우리는 여러 통계분석을 수행할 수 있다는 장점
확률 밀도 함수
- 연속확률변수의 분포를 나타내는 함수
$$ \int _{∞}^{−∞}f(x)dx = 1$$
- 확률 밀도 함수 f(x)와 구간 [a,b]에 대해서 확률 변수 X가 구간에 포함될 확률
$$ \int _{a}^{b}f(x)dx $$
$$ f(x) = N(x|μ, σ^2) ={1 \over σ \sqrt{2\pi}}e^{-(x-μ)^2 \over 2σ^2}$$
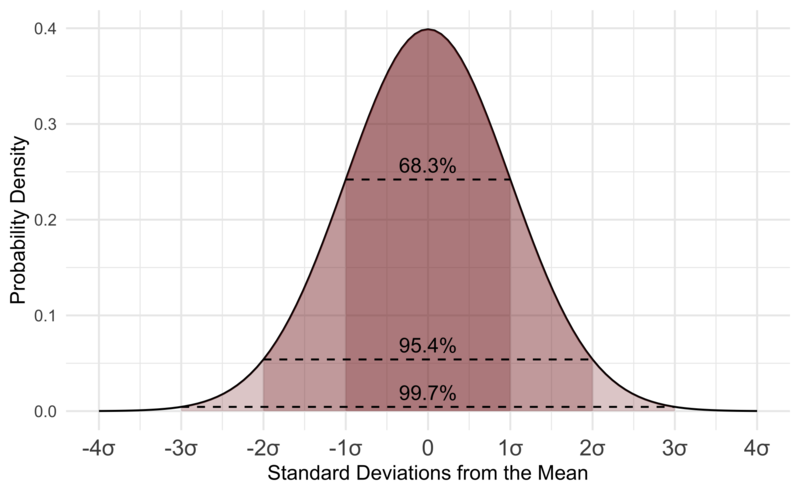
정규분포곡선
- 확률변수X의 평균은 μ이고 표준편차 σ 인 위 확률밀도함수를 가질 때 확률변수X는 정규분포를 따른다
- 정규분포곡선에서 각각의 분포마다 평균이나 분산은 모두 다르지만, 각각의 평균에서 표준편차의 실수배한 위치에서 확률밀도함수의 y값은 일정

표준정규분포( z-분포 곡선)
- 표준정규분포는 평균이 0, 표준편차가 1로 표준화 한 정규분포
$$ Z = {X - μ \over σ} $$
- X : 표준화 하기 전 원래 자료의 수치
- Z : 표준화된 후 수치
- μ : X의 평균
- σ : X의 표준편차
$$ f(x) = N(0,1) ={1 \over \sqrt{2\pi}}e^{-z^2 \over 2}$$